Brojevi u starom Egiptu – II deo

Starim Egiptom su vladali faraoni, nasledni vladari, koji su pripadali dinastijama koje su neobično dugo trajale. Središte države se uvek nalazilo u donjem toku Nila na prostoru između danas najvećih egipatskih gradova Kaira i Aleksandije. Glavni centri učenosti su bili među sveštenstvom. Egipatska matematika, pre svega aritmetika, bila je okrenuta praktičnim pitanjima državne uprave (prikupljanje poreza) i poljoprivrede (razmeravanje zemljišta posle poplava)

Aripmetiku egipatske matematike prikazaćemo koristeći hijeroglifsko zapisivanje brojeva koje smo opisali u prethodnom članku. link

Sabiranje

Sabiranje u ovom sistemu se postiže sakupljanjem simbola sabiraka u jednu celinu i pretvaranjem svakih deset istih u jedan simbol veće vrednosti.

Oduzimanje

Oduzimanje se suštinski zasniva na uklanjanju simbola od kojih je sačinjen umanjilac. Ovaj postupak je komplikovan ukoliko simbola umanjioca ima više nego istih tih simbola u umanjeniku. Ilustracija oduzimanja 63-38 je data na crtežu.

Množenje

Množenje dva broja je vršeno uzastopnim udvostručavanjem, a zatim sabiranjem onih stepena broja 2 koji u zbiru daju broj kojim se množi. Princip je bio da se uvek udvostručuje veći broj. Jedino odstupanje od ovakvog množenja je slučaj kada se množi dekadnom jedinicom. U tom slučaju se odgovarajući simboli zamenjuju simbolima odgovarajuće deset puta veće dekadne jedinice.

Deljenje

Deljenje je zahtevalo upotrebu množenja ili još češće razlomaka. Ukoliko je rezultat deljenja ceo broj (tzv. jednostavno deljenje) gledano je kojim brojem je potrebno pomnožiti delilac da bi se dobio deljenik.

Razlomci u Egipatskoj matematici su bili ograničeni na jedinične razlomke uz izuzetak često upotrebljavanog razlomka i ređe upotrebljavanog . Jedinični razlomci su razlomci oblika , gde je prirodan broj.Razlomci su hijeroglifima bili predstavljeni stavljanjem simbolakoji je predstavljao ,,usta” i značio ,,deo”.Primeri razlomaka dati su na slikama.

Abeceda računanja sa razlomcima počinjala je uz poznavanje ovih jednakosti

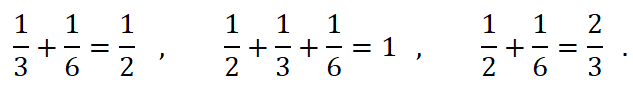
Važna pomoć pri računanju bile su tablice vrednosti brojeva 2/n za sve neparne brojeve n od 3 do 101. U ovim tablicama postojale su čitave klase brojeva koje sui male jedinstveno predstaljanje. Tako su svi brojevi oblika 2/3n predstavljani kao 1/2k + 1/6k , itd.

Kao što smo već rekli, sveštenici su bili ti koji su vladali matematičkim znanjima. Deo tih znanja je bio i Egipatski kalendar. Naime, još 3000 godina pre Hrista egipatska godina trajala je 365 dana. Kako je egipatska civilizacija dugo trajala, oni su stigli da primate da se za njihov život najvažnija prirodna pojava-, izlivanje Nila, stalno pomera i da se posle 1460(=4∙365)godina vraća na početak. Zaključak su onda brzo izveli : godina traje 365,25 dana.Tako su egipatski sveštenici još 238. godine pre nove ere zakljičili sa svaka četvrta godina treba da bude duža za 1 dan,tj. da bude prestupna.

Uticaj religije na egipatsku matematiku možemo videti na sledećem primetu. Stari Egipćani su verovali da ih simbol “Rx” , tj.simbol boga Horusa štiti od zla. Zato su i u matematiku ugradili simboliku pa su razvili i svojevrsni brojevni sistem koji se koristio za prepisivanje lekova, podelu zemlje ili semena.

Razlomke su pravili tako što su kombinovali pojedine delove boga Horusa.Svaki deo oka imao je različitu vrednost. Celokupni simbol oka imao je vrednost 1, a celi sistem se temeljio na podeli na polovine.Prikaz je dat na slici.